To determine the role of luck in winning a Euchre tournament, I wanted to see how consistently good or bad a player’s hand is likely to be over the course of the number of hands dealt. What is the probability of the deal being so consistently good as to win a certain percentage of the hands over the course of the evening?
I immediately think of Monte-Carlo simulations when I see this kind of question. In this case, I simulated the cards dealt to each player. Ideally, I would also simulate the bidding process and the play of each hand with equally-skilled Euchre agents to determine the winner. However, that requires a rather complex model. Often, it’s possible to gain insight into a problem using a simplified model. In this case, I simplified the problem by eliminating bidding and finding a way to compare hands without simulating playing them.
First, I randomly assigned trump. Then, I gave each card a value corresponding to the number of cards in the deck that it beats. For instance, the right Bauer (Jack of the trump suit) beats all 23 other cards in the deck, so it gets a value of 23. To determine the winner of the round, I considered each team’s hands together and compared between teams by looking at the total value of their cards. In order to win a hand, a team must take at least three tricks of the five played. That is, the partners must have cards that beat at least 9 other cards. Therefore, I gave the team a win if their hands had a total value of at least 9 more than their opponents’ hands.
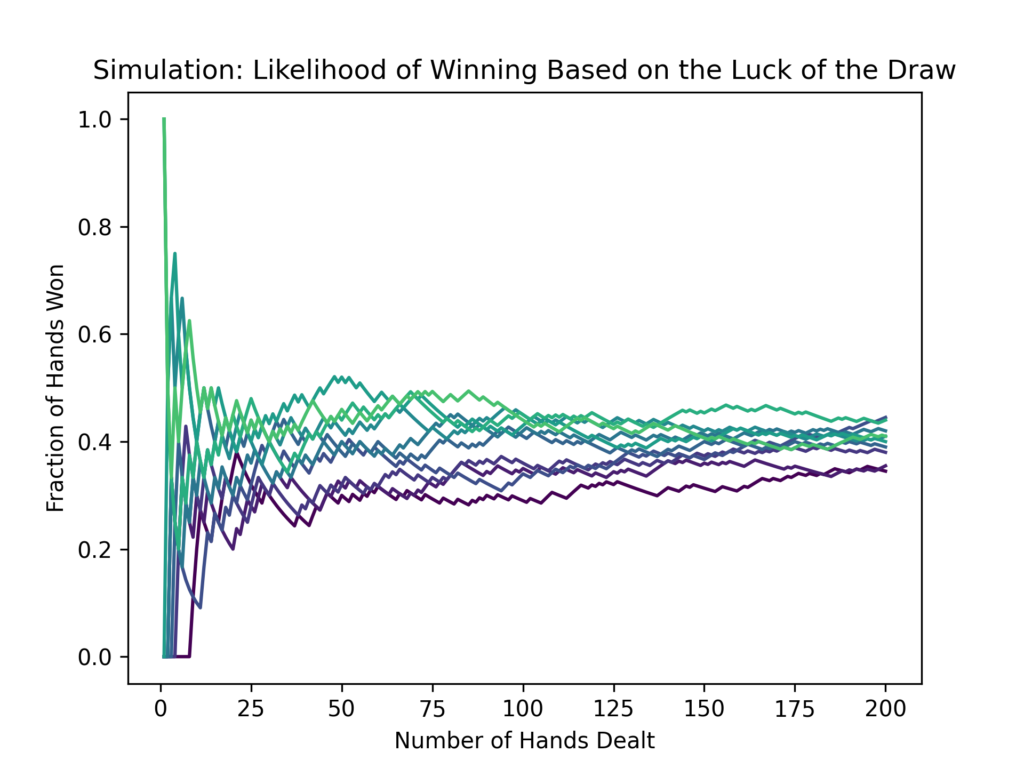
I ran the simulation under these conditions. Whether I simulated the conditions 10 or 100 times, the conclusions were similar. For the first 10 hands, many of the simulations had a high proportion of winning or losing hands. After about 100 hands, the simulations tended towards 40% wins, with a range from 30% to 50%. Unsurprisingly, when I changed the simulation so a win was scored for a team when the total hand value was simply higher than their opponents’, the result was similar, except that it converged around 50% wins. A player likely plays fewer than 10 hands in any given game. Over the course of a tournament any player could easily play more than 50 hands. For comparison, the tournament analyzed in the previous posts consisted of 4 hands per game for a total of 44 hands over the course of the evening. I interpret this to mean that winning any game is highly random and determined primarily by the luck of the draw. However, over the course of an entire tournament, a player winning over 60% of their hands owes their success to something beyond luck—likely skill.


